算法:高精度运算
我们知道每种数据类型的储存空间是有限的,如果我们要储存非常大的数可以用long long,更大则unsigned long long,再大就是有些编译器提供的_int128类型,但是要是比这还要大呢?我们就需要用到高精度运算,用数组来模拟非常大的整数。
我们只要定义一个数组,把数字分别放入数组序列中就可以储存非常大的数。
接下来我们看看怎么使用高精度运算。
(注意以下都是我个人的解法,不一定是最优解,借鉴学习即可)
A+B
**题目:**高精度加法,相当于 a+b problem,不用考虑负数。(洛谷P1601题)
输入a和b,然后输出a+b,太简单了!但是,题目要求的是高精度加法,也就是说输入的a和b是非常大的,我们要使用高精度才能储存该数进行处理。
首先我们看看加法的竖式
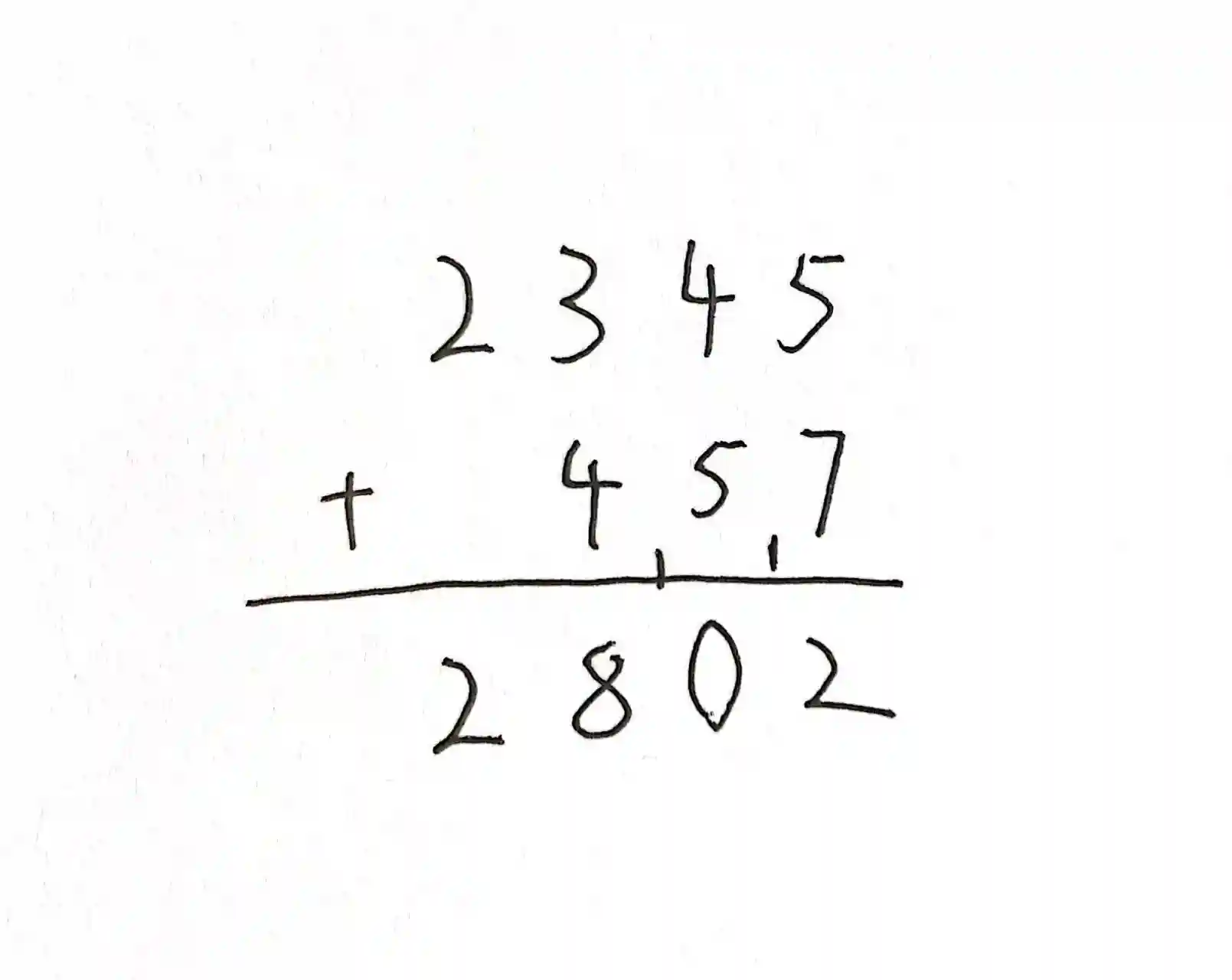
如果超过10就要向下一位进位,进位的数字和下一位的值相加
#include<iostream>
#include<string>
#include<algorithm>//包含max函数
using namespace std;
int A[500], B[500], C[500];//这个定义必须放在主函数外!!!这样它才会初始化,我被这个坑惨了
int main(){
string a,b;
cin >> a >> b;
int lena = a.length(), lenb = b.length();
int len = max(lena, lenb);
//把字符变成对应的数字,并倒序存入
for (int i = 0; i < lena; i++) A[i] = a[lena-1-i] - '0';
for (int i = 0; i < lenb; i++) B[i] = b[lenb-1-i] - '0';
//相加并处理进位
for (int i = 0; i < len; i++) {
//相加
C[i] += A[i] + B[i];
//进位
C[i + 1] = C[i] / 10;
C[i] = C[i] % 10;
}
//如果进位使得位数增加,我们就多输出一位
if (C[len]) len++;
//因为我们之前是倒序存入,所以现在倒序输出就又正了
for (int i = len-1 ; i >= 0; i--) cout << C[i];
return 0;
}
A*B
**题目:**给出两个非负整数,求它们的乘积。每个非负整数不超过 10^2000^(洛谷P1303题)
还是一样,看似是道弱智题,但是我们要注意输入值的范围,数值非常大,再加上要相乘,很容易就会超过我们数据类型范围,所以又要用到我们的高精度方法。
算乘法,我们就先复习下乘法竖式
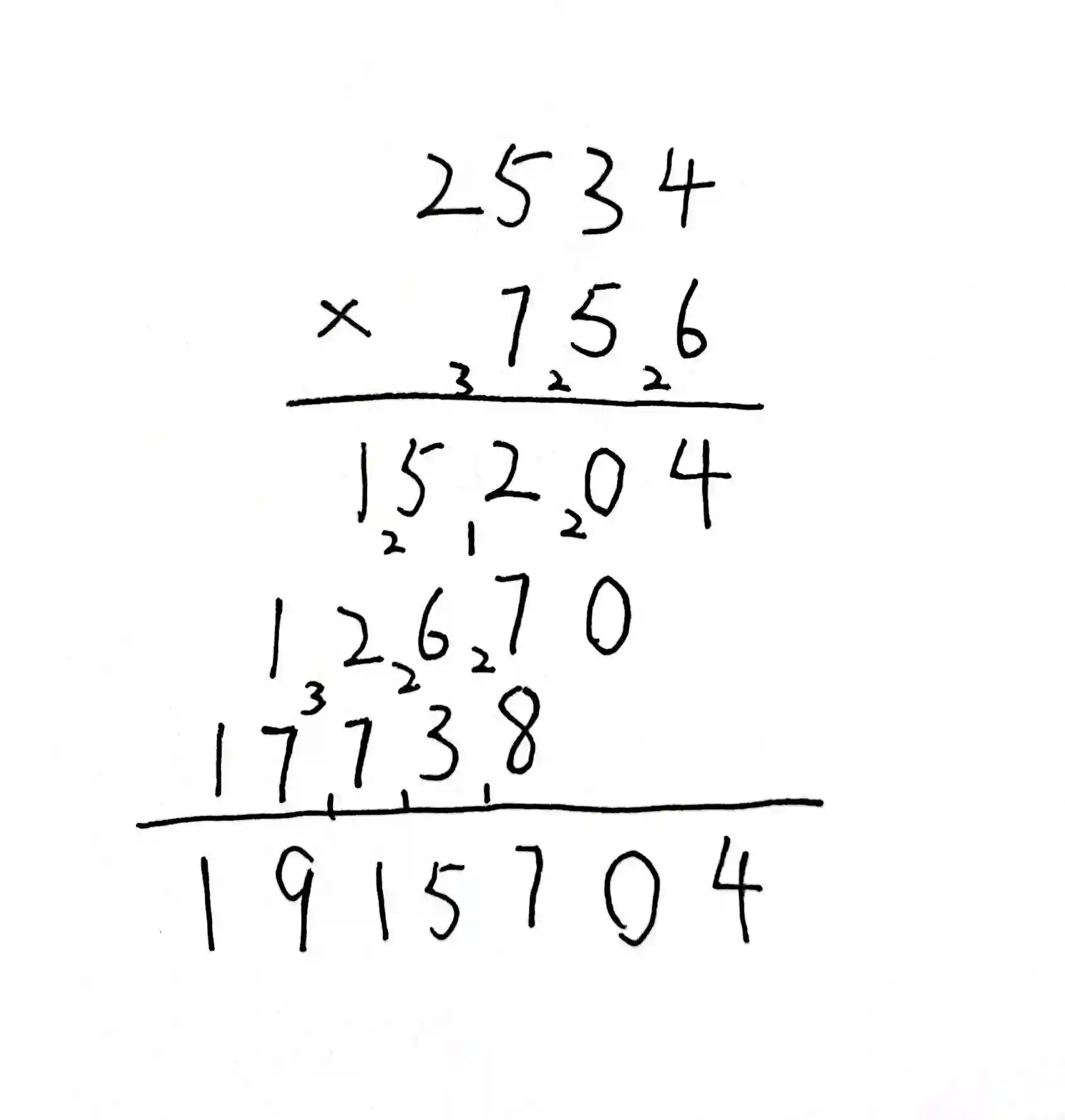
几个需要知道的点
- 和加法非常像,也是超10进位。
- 这里有个很重要的规律,我们倒着数,第一个数的i位乘第二个数的j位,它们的乘积会到第(i+j-1)位上。
- 乘积的位数不超过两数的位数之和。
知道了这个,我们就可以开始了。
#include<iostream>
#include<string>
using namespace std;
int A[5000], B[5000], C[5000];
int main(){
string a, b;
cin >> a >> b;
int lena = a.length(), lenb = b.length();
//转化成对应数字并倒序存入
for (int i = 1; i <= lena; i++) A[i] = a[lena - i]-'0';
for (int i = 1; i <= lenb; i++) B[i] = b[lenb - i]-'0';
//计算乘积
for (int i = 1; i <= lena; i++) {
for (int j = 1; j <= lenb; j++) C[i + j - 1] += A[i] * B[j];
}
int len = lena + lenb;//乘积的位数不超过两数的位数之和
//处理进位
for (int i = 1; i <= len; i++) {
C[i + 1] += C[i] / 10;
C[i] %= 10;
}
//去掉多余输出的位数
while (!C[len]) len--;
//特殊情况,乘积等于0
if (len < 1) len = 1;
//输出
for (int i = len ; i >= 1; i--) cout << C[i];
return 0;
}
阶乘之和
题目描述
用高精度计算出 $S = 1! + 2! + 3! + \cdots + n!$($n \le 50$)。
其中 ! 表示阶乘,定义为 $n!=n\times (n-1)\times (n-2)\times \cdots \times 1$。例如,$5! = 5 \times 4 \times 3 \times 2 \times 1=120$。
输入n,输出s。(洛谷P1009题)
这道题可以说是前两道题的结合。
这是我的解法,因为这道题较特殊,所以可以做到比前两道的代码还短,可能有点抽象,要仔细思考
#include<iostream>
using namespace std;
int main()
{
int i, A[1005] = { 0 }, B[1005] = { 0 }, n, j;
cin >> n;
A[0] = B[0] = 1;
//这个循环是外面的加法
for (i = 2; i <= n; i++) {
//阶乘的相乘
for (j = 0; j < 100; j++)
B[j] *= i;
//阶乘的进位
for (j = 0; j < 100; j++)
if (B[j] > 9) {
B[j + 1] += B[j] / 10;
B[j] %= 10;
}
//每算完一个阶乘就加进结果并处理进位
for (j = 0; j < 100; j++) {
A[j] += B[j];
if (A[j] > 9) {
A[j + 1] += A[j] / 10;
A[j] %= 10;
}
}
}
//去除多余的位数
for (i = 100; i >= 0 && A[i] == 0; i--);
//输出
for (j = i; j >= 0; j--) cout<< A[j];
return 0;
}
灵活掌握,举一反三才能在程序竞赛中绽放自我。